Machine Learning : MPG-Partners propose une nouvelle méthode

 

Dans le contexte d’IA-bashing[1] actuel, MPG Partners propose une approche simple, efficace, robuste et surtout bien comprise.

Escroquerie, impasse[2]…plus un jour ne se passe sans que ne soient décriées les dérives liées à l’intelligence artificielle (IA). On retient de ces critiques qu’elles se focalisent sur l’absence de socle théorique : les méthodes IA sont avant tout empiriques. On sait montrer qu’elles fonctionnent dans certains cas, sans pouvoir réellement expliquer pourquoi. Cela laisse libre cours aux interprétations, et donc aux pratiques, les plus fantaisistes.

Dans ce contexte, MPG Partners propose une méthode type Machine Learning (ML) simple, efficace, robuste, universelle, et surtout bien comprise, parce que disposant d’une théorie mathématique solide. Pour établir ses performances, nous la comparons aux meilleures implémentations open-source utilisées par la communauté IA: cette approche s’avère être meilleure que les méthodes de type réseau de neurones.

  

Des aspirations légitimes

Les applications visées par le Machine Learning sont aujourd’hui innombrables. Cela est vrai quelques soient les secteurs industriels, et plus particulièrement en Finance : le KYC (connaître sa clientèle), le risque de crédit, la valorisation et l’estimation des risques ne sont que la partie émergée de l’iceberg des applications potentielles. Et les algorithmes proposés par la communauté IA produisent déjà des résultats convaincants … si l’analyse amont du problème posé est faite correctement bien sûr.

Les aspirations de l’Intelligence Artificielle ou du Machine Learning semblent donc bien légitimes. Cependant, le manque de socle théorique est une critique majeure : sans cette brique essentielle dans le développement d’une technologie, comment en comprendre ou en expliquer les résultats ? Comment convaincre qu’un algorithme est performant si on n’en connaît pas les limites ?

 

Des technologies existantes et éprouvées

Cette critique est d’autant plus justifiée qu’il existe des approches alternatives qui sont très efficaces et solides, mais en marge de celles utilisées par la communauté IA. En fait, ces outils existent depuis longtemps. En effet, notre équipe R&D a développé un framework[3], dédié à l’analyse des risques en Finance, qui s’appuient sur des méthodes de Machine Learning[4] innovantes toutes aussi solides numériquement que théoriquement. Il repose sur des théories bien établies, comme celles des noyaux reproducteurs[3](RHKS) ou du transport optimal. Techniquement, pour le Machine Learning, la méthode que nous proposons est proche des machines à vecteur de support (support vector machine).

Mais comment un framework, dédié à l’analyse des risques en Finance, peut-il prétendre à être également une plate-forme de Machine Learning ? Parce que ce framework a été développé pour répondre à un problème bien particulier : la malédiction dimensionnelle – pour la résolution numérique des équations aux dérivées partielles (EDP). Dans notre contexte, la malédiction dimensionnelle veut dire qu’il n’existait pas de méthode EDP en grandes dimensions. En finance, cela implique que l’utilisation des EDP ne pouvait se faire avec plus de trois ou quatre sources de risques. C’est ce point que nous avons levé, notre contribution majeure pouvant se résumer à l’art et la manière de représenter le plus efficacement possible une fonction arbitrairement complexe avec un ordinateur.

Or, pour représenter une fonction, nous utilisons des machines à vecteur de support, parce que nous avons prouvé[4] qu’elles sont les meilleurs possibles, dans un sens très précis. Donc ce framework a été bâti sur un concept de machines à vecteurs de support[5], qui est une technologie employée pour le Machine Learning.  Ainsi, nous pouvons aujourd’hui :

• Construire facilement des machines d’apprentissage.
• Justifier théoriquement de la pertinence de nos résultats avec notre recherche.
• Et surtout nous pouvons combiner ces machines d’apprentissage, en les adaptant légèrement bien sûr, avec tous les algorithmes originaux et analyses que nous avons développés pour la résolution des équations aux dérivées partielles.

Notamment, nous présentons dans cet article le résultat d’une petite partie des fonctionnalités que nous sommes en train de tester dans le cadre du Machine Learning, grâce à l’éclairage de notre recherche théorique sur les EDP.

Mais comment se compare notre approche à celles proposées par la communauté IA ?

 

Un Benchmark de cette approche

Pour y répondre, nous avons effectué un test, comparant nos machines d’apprentissage avec la meilleure machine provenant de la communauté IA à notre disposition, qui se trouve être celle proposée par Tensorflow / Keras, un framework de réseaux de neurones développé par la société Google, dédié au Machine Learning. Ce comparatif consiste à réaliser un test standardisé, largement répandu, pour évaluer les machines à apprentissage renforcé : le test de reconnaissance de caractères écrits (MNIST). La description du test, technique, est reléguée en annexe.

Les conclusions de ce comparatif sont les suivantes :

1. Les taux de reconnaissance de nos machines sont meilleurs, et d’un facteur d’échelle. Pour le test MNIST présenté, nous obtenons sans aucun effort particulier des taux de reconnaissance dépassant les meilleures implémentations des machines à réseaux de neurones de plusieurs pour cent (cf annexe tables 1 et 3), ce qui est énorme pour ce type de test. Ce point est important notamment pour réduire par exemple les faux positifs dans ces algorithmes.
2. Notre framework se résume aujourd’hui à une seule fonction, permettant d’aborder tous les problèmes d’apprentissage supervisé de manière homogène et universelle.

C’est une approche extrêmement robuste, qui ne nécessite aucun paramétrage

3. Nous exhibons un indicateur, que nous appelons l’erreur de discrépance, qui est une sorte de « distance » entre deux ensembles de points, introduite dans cet article. Cet indicateur permet de calculer un taux de reconnaissance théorique, correspondant au cas le pire. Ce taux de reconnaissance théorique correspond très bien au taux que nous calculons empiriquement.

Cela signifie que nous comprenons et pouvons expliquer pourquoi et comment nos machines d’apprentissage fonctionnent, ainsi que leurs limites

4. Les temps d’apprentissage de nos machines sont plus importants que celles proposées par les machines type réseau de neurones (cf annexe table 2 et 3, colonne « times »). Cependant nous disposons toujours d’une marge de progression : nous pouvons partir de cette première approche pour optimiser une machine d’apprentissage en la spécialisant à un problème donné.

Par exemple, nous proposons en annexe une méthode qui permet de réduire les temps d’apprentissage de nos machines, au détriment de la précision. Nous obtenons alors une machine très comparable en termes de performance à celle de Keras / Tensorflow. Nous pouvons donc adapter nos machines aux besoins utilisateurs si besoin il y a, par exemple si les temps d’apprentissage sont un facteur limitant.

 

Conclusion

MPG Partners a mis au point des machines d’apprentissage qui ne reposent pas sur des technologies type réseaux de neurones, mais qui s’apparentent à des machines à vecteurs de support. On ne peut qu’en conseiller l’utilisation : elles sont plus précises, plus simples d’utilisation, et plus générales que celles proposées par la communauté IA aujourd’hui. Elles sont également mieux comprises, ce ne sont pas des « boîtes noires ».

De plus, nous disposons d’une expérience solide dans l’utilisation de ces technologies. Nous les utilisons pour résoudre des problématiques issues des mathématiques financières, et également provenant d’autres secteurs industriels. En finance, ce framework nous a permis de répondre à des besoins utilisateurs concrets : par exemple comment optimiser d’un facteur d’échelle les méthodes existantes de valorisation, mais également de calcul de métriques de risques complexes, type VaR (Value at Risk), ES (Expected Shortfall) ou CVA (Credit Value Adjustment)[6]. Ou alors répondre à des questions ouvertes comme le calcul de stratégies complexes en ALM[7].

Ces expériences nous permettent non seulement d’être pertinents, mais également de proposer des approches innovantes dans le cadre du Machine Learning, domaine dans lequel nous avons encore une marge de progression très importante grâce à notre recherche.

 

 

Annexe: benchmark CoDeFi vs Keras / Tensorflow

Dans cette annexe, un peu plus technique, nous comparons une de nos machines d’apprentissage renforcé (supervised machine learning) à une solution largement utilisée par la communauté AI, TensorFlow / Keras, dans le cadre d’un benchmark très largement utilisé, celui de la MNIST.

Décrivons rapidement l’objet de ce test : il propose un ensemble de M images d’apprentissage, représentant des chiffres manuscrits, chaque image étant associée à un label de « 0 » à « 9 ». Dans un premier temps la machine « apprend » sur cet ensemble M. Dans un deuxième temps, elle doit pronostiquer le chiffre représenté par un ensemble de 10000 nouvelles images. Ce chiffre est comparé avec celui de chaque image. Cela permet d’établir un « score », qui est un nombre compris entre 0 et 1, représentant le nombre de labels correctement pronostiqués divisés par 10000. Donc plus ce score est élevé, meilleure est la précision de la machine d’apprentissage. Bien sûr, le temps d’apprentissage et de pronostic est noté, cet indicateur étant important pour caractériser la performance globale de la machine d’apprentissage : plus il est faible, meilleur c’est !

Nous voulons comparer deux méthodes:

• La première utilise directement une machine à vecteur de support construite sur notre framework CoDeFi.
• La deuxième utilise le framework Tensorflow / Keras, un framework développé par la société Google, dédié au machine learning. Il consiste en un réseau de neurones avec un layer, qui est un ensemble de N=200 neurones [10] Il s’agit d’un algorithme proposé en standard dans la section « quickstart for beginners » pour illustrer les capacités de Tensorflow, et est fortement optimisé. Il est entièrement accessible et décrit ici.

Notre benchmark dépend donc de deux entiers : M le nombre d’images dans l’ensemble d’apprentissage, mais aussi d’un autre entier, N inférieur à M, qui donne le nombre de neurones utilisés pour Keras / TensorFlow. Pour notre méthode, nous disposons également de l’équivalent de ce nombre de neurones N : c’est le nombre d’images que nous utilisons parmi les M de l’ensemble d’apprentissage.

Nous avons fait attention aux paramètres du benchmark : les deux méthodes sont configurées pour fonctionner CPU- parallèle, nous utilisons la même machine pour nos tests, et aucune technique tirant partie des données en entrée (type filtre) n’est utilisée.

Voici le premier résultat de ce test concernant Keras: il s’agit d’un tableau constitué de scores et de temps d’exécution, exprimés en secondes.

 

Voici maintenant le deuxième résultat, correspondant à notre méthode, avec M=N. En plus des scores (comp. Upper bound) et du temps d’exécution (times), nous avons noté un indicateur (theo. Upper bound), qui correspond à l’erreur de discrépance, une notion introduite dans cet article.

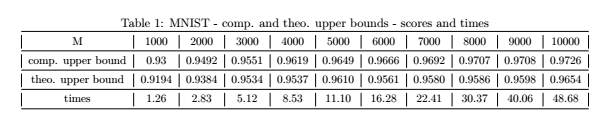
Commentons ces résultats :

• Tout d’abord on remarque que notre machine d’apprentissage donne systématiquement de meilleurs scores que Keras / Tensorflow. Remarquez également que pour par exemple 10000 images, la différence est de taille : 97,26% comparée à 95,05% est un énorme gain pour ce type de test : nos machines sont meilleures en terme de précision, et ce d’un facteur d’échelle.
• D’autre part, on voit que l’erreur de discrépance (« theo. Upper bound ») est un indicateur qui explique nos résultats. Il permet de se faire une bonne idée de la précision de nos machines avant même d’en calculer le score.
• Cependant les temps d’apprentissage de nos machines sont plus lents.

Dans le test suivant, nous proposons de modifier légèrement notre algorithme en prenant N = 500, et non N=M comme dans le test précédent. Les résultats sont table 4. Ils montrent que la machine d’apprentissage renforcée est maintenant comparable à celle de Keras / Tensorflow, autant en termes de performance que de temps d’exécution.

 

 

[1] L’intelligence artificielle est « dans l’impasse », le monde 24 décembre 2019

[2] L’intelligence artificielle est bien aujourd’hui une escroquerie !, le monde 24 novembre 2019

[3] CoDeFi, un nouvel algorithme pour la mesure des risques : C.R.A.S., Ser. I (2017), http://dx.doi.org/10.1016/j. crma.2017.05.003 ]

[4] The Transport-based Mesh-free Method (TMM): a review. To appear in Wilmott magazine, September 2020.

[5] Bien que notre framework ait été développé indépendamment des théories RHKS, il s’avère en être proche.

[6] https://arxiv.org/abs/1911.00795

[7] Il est possible d’intégrer n’importe quel réseau de neurones dans une machine à vecteur de support. L’inverse n’est pas vrai. En résumé, les machines à vecteur de support sont plus générales que les machines à réseaux de neurones.

[8] Nous avons développé notamment, pour un cas utilisateur, un prototype de calcul de risques de grands portefeuilles d’Autocalls multi-sous jacents.

[9] https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3454813

[10] C’est le nombre de neurones qui nous a semblé donné les meilleurs résultats pour ce test MNIST, avec le réseau proposé en standard du framework Keras / Tensorflow.